Leitrad

 

Um dieses zu konstruieren, benötigt man lediglich die folgenden Werte: Radius am Eintritt , Schaufelzahl , Anstellwinkel , Schaufeldicke am Eintritt , Eintrittshöhe in den Leitraddiffusor , dessen Länge L und Öffnungswinkel sowie den Radius am Laufradaustritt . Die Schaufelform erhält man wie nachfolgend beschrieben (Abbildung 2.6 zeigt nach diesen Vorgaben konstruierte Schaufeln):

1. Der Mittelpunkt des Leitrades wird auf den Nullpunkt (0, 0) gelegt.
2. Der Mittelpunkt des Kreises der Leitradspitze mit dem Radius wird auf den Punkt mit den Koordinaten () gelegt.
3. Koordinaten des Punktes A:

   

4. Koordinaten des Punktes E:

   

5. Koordinaten des Punktes :

   

6. Koordinaten des Punktes :

   
   
   

   

7. Durch Drehung um den Winkel von und um den Nullpunkt erhält man die Koordinaten der Punkte C und D:

   

   

8. Radius :
   
   
9. Der Punkt B ist der Schnittpunkt des Kreises mit einer Geraden, die durch den Punkt A geht und unter dem Winkel () verläuft:

   
   
   

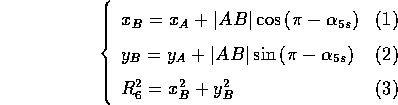
   Werden in Gl. (3) und durch die rechten Seiten der Gln. (1) bzw. (2) ersetzt, so erhält man eine Gl. mit der Länge der Strecke als einziger Unbekannten:

   
   
   

   Für läßt sich somit schreiben:

   
   
   

   die andere Lösung ist für die Konstruktion der Schaufel bedeutungslos. können nun mit Gl. (1) bzw. (2) bestimmt werden.

10. Die dimensionslosen Koordinaten der fünf Punkte A, B, C, D, E liegen damit fest und müssen nur noch mit multipliziert werden.
11. Der Verlauf der Schaufelkontur zwischen D und E kann durch eine Kurve beschrieben werden, welche die folgenden Bedingungen erfüllt:

    

Geeignete Kurven sind z.B. Ellipsen, Kurven der Form (in einem neuen Koordinatensystem u,v, welches gegenüber x,y um () gedreht ist und dessen Nullpunkt in liegt) und Splines (nicht jedoch Kreise). Welche davon gewählt wird, hängt von den Fähigkeiten des verwendeten CAD-Systems ab. Im Programm werden kubische Bézier-Splines (Funktion CDC::PolyBezier) verwendet, dafür sind genau vier Punkte erforderlich. Die Splines verlaufen genau durch den ersten bzw. letzten Punkt (D bzw. E), der Kurvenverlauf dazwischen wird durch zwei Stützpunkte beschrieben. Diese beiden Punkte sind die Mittelpunkte der Strecken DH bzw. HE, der Punkt H ist der Schnittpunkt der Geraden CD mit der Parallelen zu AB durch E. Die ursprünglich geplante Verwendung von Ellipsen wäre nicht ohne weiteres möglich gewesen, da die vorhandenen Funktionen nur die Ausgabe ganzer Ellipsen erlauben.