Ausgehend von der Forderung, daß die Eintrittshöhe 
bei Beginn des eigentlichen Diffusorteils des Leitrades ungefähr mit der
Breite an der gleichen Stelle 
übereinstimmen soll (maximaler
Diffusor-Wirkungsgrad unter ansonsten gleichen Bedingungen), liegt
somit fest. Eine Abweichung davon muß lediglich dann gemacht
werden, wenn diese Höhe auf eine zu große Leitschaufelzahl führen
würde (
,,Blechschaufel``, für kleine , meist bei hohen Stufen-Druckverhältnissen).
Dies ist jedoch nicht von großem Nachteil, da der
Wirkungsgrad für die sich aus dieser Bedingung ergebenden größeren
-Werten nur unwesentlich abfällt
(ein Verhältnis 
ist dagegen besonders
ungünstig, man vgl. mit [Tra88] sowie Abbildung 2.5,
die 
-Werte des mittleren bzw. rechten Bildes).
Die Forderung nach guten Wirkungsgraden führt weiterhin auf einen
Öffnungswinkel des Diffusors 
in der Größenordnung
. Wählt man für die
Form der Leitschaufel die einfache, gerade ,,Blechschaufel`` mit einer über
der ganze Länge gleichbleibenden Dicke, so liegt damit
bereits auch die Leitschaufelzahl fest: 
,
z.B. 
für 
,
für 
,
und 
für 
.
Für eine keilförmige Leitschaufel
mit gekrümmter Saugseite im Einlaufbereich erhält man die
Schaufelzahl aus der folgenden Beziehung
wobei der erhaltene Werte gerundet werden muß,
mit dem Versperrungsmaß durch
Grenzschicht 
aus Abbildung 2.3 (beim ersten Schleifendurchlauf müssen
, 
und geschätzt werden,
, kennzeichnen die aus der schaufellosen
Verlustrechnung mit vergrößertem Reibungs- bzw. Dissipationskoeffizienten
erhaltenen Werte).
Den für Abbildung 2.3 benötigten Umsetzungsgrad
erhält man aus
Für den Anstellwinkel
der Schaufeln 
wählt man einen Wert, der gleich oder wenig größer als
der Wert des mittleren Zuströmwinkels des Mediums 
ist
(Winkeldifferenz 
,
ansonsten werden die erhaltenen Ergebnisse aus der Verlustrechnung zu
unsicher, es müssten Informationen über den Wert der Versperrung durch
Ablösung bzw. Totwasser vorliegen).
Der Vorteil einer positiven Winkeldifferenz ist eine zu höheren
Durchsätzen 
verschobene Sperrgrenze, die für hohe
Druckverhältnisse sehr nahe am Auslegungspunkt liegt.
Der Nachteil dabei ist jedoch eine ebenfalls zu höheren
Durchsätzen (näher an den Auslegungspunkt) verschobene Pumpgrenze.
Diese Winkeldifferenz muß bei der Ermittlung der Eintrittshöhe
berücksichtigt werden (
, jedoch
sollte man darauf achten, daß für eine festliegende Schaufelzahl
bzw. einen festliegenden Anstellwinkel nicht beliebige Werte möglich
sind):
Der im Einlaufbereich des Leitrades entstehende Reibungsverlust kann
[Tra88] zufolge nach dem in Abschnitt 4.3
beschriebenen Verfahren ermittelt werden, die vergrößerte
Oberfläche durch die Schaufeln wird im Reibungskoeffizient 
und
im Dissipationskoeffizient 
berücksichtigt. Beide
werden mit dem folgenden Ausdruck multipliziert:
Mit den so ermittelten Werten für das Druckverhältnis 
und das Dichteverhältnis 
kann der Reibungsverlust
bestimmt werden:
Bedingt durch die ungleichmäßige Strömung (Abweichungen der
Geschwindigkeitsrichtung von der mittleren Richtung bis ca.
) ergibt sich
selbst für den optimalen Anstellwinkel der Schaufeln
ein Stoßverlust, der [Tra88] zufolge aus der folgenden
Beziehung abgeschätzt werden kann:
Wenn Anstellwinkel der Schaufeln und mittlere Geschwindigkeitsrichtung
nicht übereinstimmen (Teillastpunkt bzw. Auslegungspunkt mit
),
kann der zusätzliche Verlust aus der folgenden
Beziehung abgeschätzt werden
wobei man 
wie bei der
Verlustermittlung des Laufrades aus Abbildung 4.4 ablesen kann.
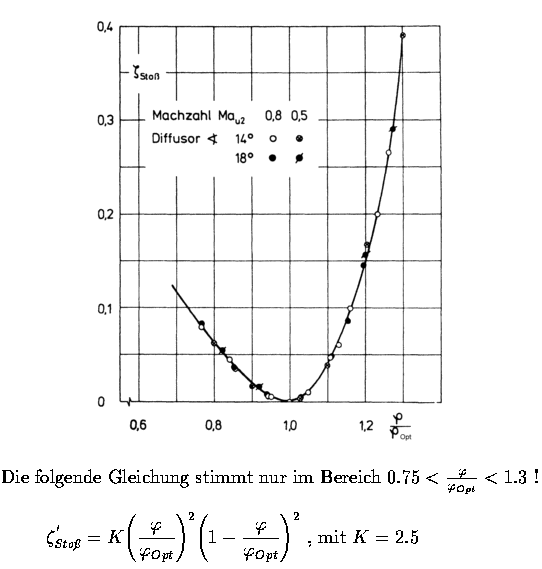
Abbildung 2.4: Stoßverlustkoeffizient des Leitrades z 'Stoß
nach [WW80]
Alternativ dazu kann der Stoßverlust des Leitrades aus der nachstehenden Beziehung ermittelt werden:
mit dem Stoßverlustkoeffizient 
aus
Abbildung 2.4.
Das Diagramm ist für die Ermittlung des Teillastverhaltens gedacht,
deswegen ist auch der Verlust über dem Durchsatzverhältnis
aufgetragen. Da sich ein solches
für einen Auslegungspunkt mit nicht bestimmen läßt,
liegt es nahe, statt dem Durchsatzverhältnis das
Verhältnis der Geschwindigkeits-Normalkomponenten zu verwenden:
, mit 
.
Die gesamte im Leitradeinlauf dissipierte Energie erhält man
durch Summation aller Energieverluste, wobei 
den Anteil des
Stoßverlustes kennzeichnet, der dem
Einlaufbereich zugeordnet wird:
Mit der Energiedissipation, dem Kontinuitätsgesetz
und mit 
kann, wie in den nachfolgenden Gleichungen
angegeben, eine Korrektur des Zustandes des Mediums erfolgen:
Diese Rechnung wiederholt man bis zur gewünschten Genauigkeit. Die oben beschriebene Korrektur kann man auch mit den in [Sch82], S. 59 angegebenen Beziehungen vornehmen, jedoch erhält man dann (zumindest für die gleiche Abbruchbedingung) geringe Abweichungen bei der totalen Normalenthalpie, die sich nicht ändern darf.
Die fehlenden Werte erhält man aus den folgenden Beziehungen:
