Mit den bekannten Hauptabmessungen des Laufrades, dem bekannten
Eintrittszustand sowie dem geschätzten oder aus vorhergehenden Rechnungen
(Iteration) bereits bekannten Austrittszustand kann der hier
entstehende Verlust nach den in [Tra88], S. 449-453 angegebenen
Unterlagen berechnet werden.
Man macht dabei folgenden Ansatz: ![]() ,
dabei enspricht
,
dabei enspricht ![]() der je Zeiteinheit dissipierten Arbeit,
der je Zeiteinheit dissipierten Arbeit,
![]() dem Dissipationskoeffizienten,
dem Dissipationskoeffizienten, ![]() der Dichte,
w der Relativgeschwindigkeit sowie dF der Fläche, an der die
Dissipation erfolgt.
der Dichte,
w der Relativgeschwindigkeit sowie dF der Fläche, an der die
Dissipation erfolgt.
Der Laufradverlust kann durch folgende Beziehung ausgedrückt werden:
![]()
wobei ![]() dem Verlust an der Radscheibe sowie an den
Schaufelflächen entspricht,
dem Verlust an der Radscheibe sowie an den
Schaufelflächen entspricht, ![]() dem Verlust an der Außenwand,
dem Verlust an der Außenwand,
![]() dem Spaltverlust und
dem Spaltverlust und ![]() dem Verlust durch nicht optimale
Zuströmrichtung.
dem Verlust durch nicht optimale
Zuströmrichtung.
Beim halboffenen Rad ist
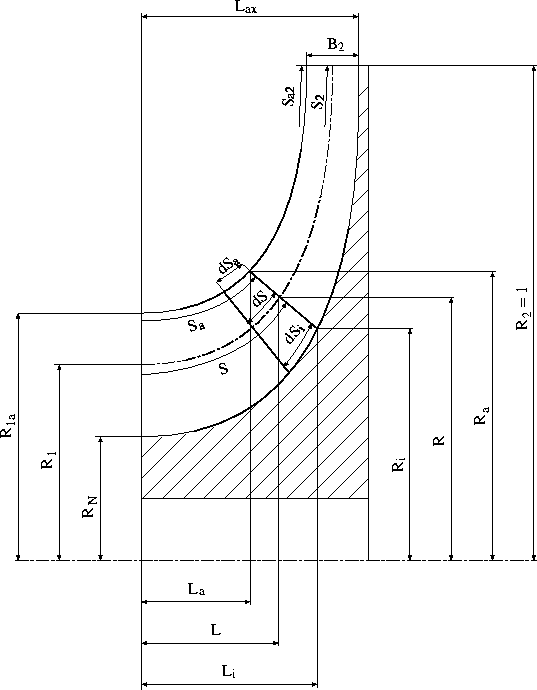
Abbildung 4.1: Bezeichnungen des Laufrades
wobei ![]() dem an der Stelle S auftretenden mittleren Strömungswinkel entspricht,
S ist dabei die von der Eintrittskante aus längs der Mittelfläche
mit dem Radius
dem an der Stelle S auftretenden mittleren Strömungswinkel entspricht,
S ist dabei die von der Eintrittskante aus längs der Mittelfläche
mit dem Radius ![]() gemessene Bogenkoordinate,
gemessene Bogenkoordinate,
![]() kennzeichnet den Anteil der lokalen Versperrung an der Radscheibe
durch die endliche Schaufeldicke, und B die lokale Kanalbreite:
kennzeichnet den Anteil der lokalen Versperrung an der Radscheibe
durch die endliche Schaufeldicke, und B die lokale Kanalbreite:
![]()
In den Gleichungen (4.2) und (4.3)
wird der Verlauf der Dichte ![]() sowie der
dimensionslosen Relativgeschwindigkeit W längs des Strömungsweges S benötigt.
Wenn angenommen werden kann, daß W entlang S linear
von
sowie der
dimensionslosen Relativgeschwindigkeit W längs des Strömungsweges S benötigt.
Wenn angenommen werden kann, daß W entlang S linear
von ![]() nach
nach ![]() abnimmt, dann gilt:
abnimmt, dann gilt:
![]()
Die Dichte ![]() erhält man aus der Kontinuitätsgleichung:
erhält man aus der Kontinuitätsgleichung:
![]()
wobei e den Anteil der lokalen Versperrung entlang der Mittelfläche
durch die endliche Schaufeldicke kennzeichnet, ![]() die lokale
Querschnittsversperrung durch Totwasser und
die lokale
Querschnittsversperrung durch Totwasser und ![]() den lokalen
Ringquerschnitt:
den lokalen
Ringquerschnitt:
Für ![]() kann man eine lineare Zunahme
entlang des Strömungsweges S annehmen
kann man eine lineare Zunahme
entlang des Strömungsweges S annehmen
![]()
oder eine lineare Zunahme mit dem Radius R
![]()
Statt eine lineare Abnahme von W anzunehmen, kann auch von einem
gleichbleibenden isentropen aerodynamischen Wirkungsgrad ![]() ausgegangen werden:
ausgegangen werden:
![]()
![]()
![]()
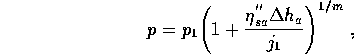
![]()
wobei als Startwert für ![]() jeweils der Wert des letzten Abschnittes
verwendet wird. Der Nachteil hierbei: es muß iteriert werden, so daß die Rechenzeit
erheblich steigt
(
jeweils der Wert des letzten Abschnittes
verwendet wird. Der Nachteil hierbei: es muß iteriert werden, so daß die Rechenzeit
erheblich steigt
(![]() ,
die Ergebnisse sind fast identisch:
,
die Ergebnisse sind fast identisch: ![]() ).
).
Der Spaltverlust läßt sich aus der folgenden empirischen Beziehung abschätzen:
![]()
mit der dimensionslosen Spaltweite ![]() .
.
Als weitere empirische Unterlagen gehen die Dissipationskoeffizienten
![]() sowie
sowie ![]() in die Verlustrechnung ein:
in die Verlustrechnung ein:
![]()
![]()

Abbildung 4.2: Diagramme zur Bestimmung des
Reibungskoeffizienten cf sowie des
Korrekturfaktors für den Radreibungsverlust CM
in Abhängigkeit von der Reynoldszahl, nach [Tra88], S. 409
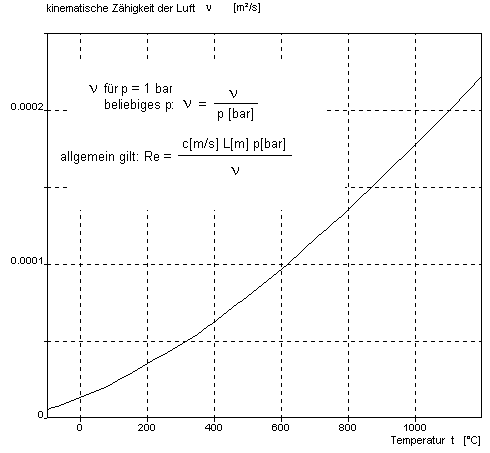
Abbildung 4.3: Kinematische Zähigkeit der Luft n(t, p),
nach [Tra88], S. 465
mit dem Reibungskoeffizienten ![]() für ausgebildete Rohrströmung, der aus Abbildung (4.2)
ermittelt werden kann. Die hierfür notwendige Reynoldszahl kann für
den Zustand am Radaustritt ermittelt werden:
für ausgebildete Rohrströmung, der aus Abbildung (4.2)
ermittelt werden kann. Die hierfür notwendige Reynoldszahl kann für
den Zustand am Radaustritt ermittelt werden: ![]() ,
mit
,
mit ![]() für Luft aus Abbildung 4.3. Ebenso
muß die relative mittlere Rauigkeit
für Luft aus Abbildung 4.3. Ebenso
muß die relative mittlere Rauigkeit ![]() in den Kanälen bekannt sein
in den Kanälen bekannt sein
![]()
mit ![]() . Vernachlässigt man
. Vernachlässigt man ![]() und
und ![]() ,
wird
,
wird ![]() 0.5% besser.
0.5% besser.
Den Verlust durch nicht optimale Zuströmung ![]() erhält man aus
erhält man aus
![]()
wobei ![]() aus Abbildung 4.4
abgeschätzt
werden kann, mit
aus Abbildung 4.4
abgeschätzt
werden kann, mit ![]() als Anströmwinkel gegen die Skelettlinie
(positiv, wenn auf die Druckseite gerichtet), und
als Anströmwinkel gegen die Skelettlinie
(positiv, wenn auf die Druckseite gerichtet), und
![]() .
.
Ein Alternative dazu ist, den Strömungswirkungsgrad des Laufrades
nur mit dem Reibungs- und Spaltverlust zu ermitteln,
und davon den Stoßverlustkoeffizienten
![]() abzuziehen
(Verlust durch nicht optimale Anströmung),
den man aus Abbildung (4.5)
in Abhängigkeit vom Durchmesserverhältnis
abzuziehen
(Verlust durch nicht optimale Anströmung),
den man aus Abbildung (4.5)
in Abhängigkeit vom Durchmesserverhältnis ![]() und vom auf das Optimum bezogenen
Durchsatz
und vom auf das Optimum bezogenen
Durchsatz ![]() erhält:
erhält:
![]()
Mit diesem korrigierten Wirkungsgrad kann der Zustand am Radaustritt ermittelt werden.
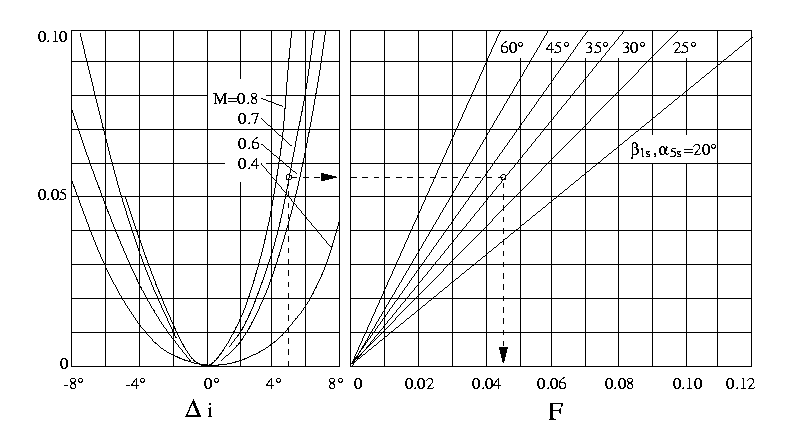
Abbildung 4.4: Diagramm zur Bestimmung von
F(Di,
M,
b1s bzw.
a5s),
nach[Tra88], S. 451
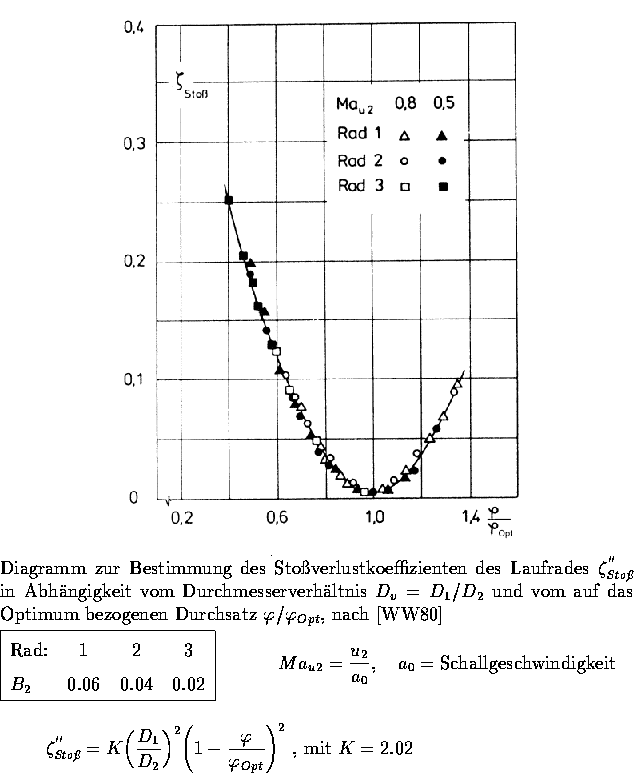
Abbildung 4.5:
Stoßverlustkoeffizient des Laufrades ![]()